割线定理（圆幂定理的称谓及内容）

圆幂定理的称谓及内容

圆幂定理是一个总结性的定理，是对相交弦定理、切割线定理、割线定理以及它们推论的统一与归纳，主要内容包括：

1.相交弦定理（图1）：圆内的两条相交弦，被交点分成的两条线段长的积相等。

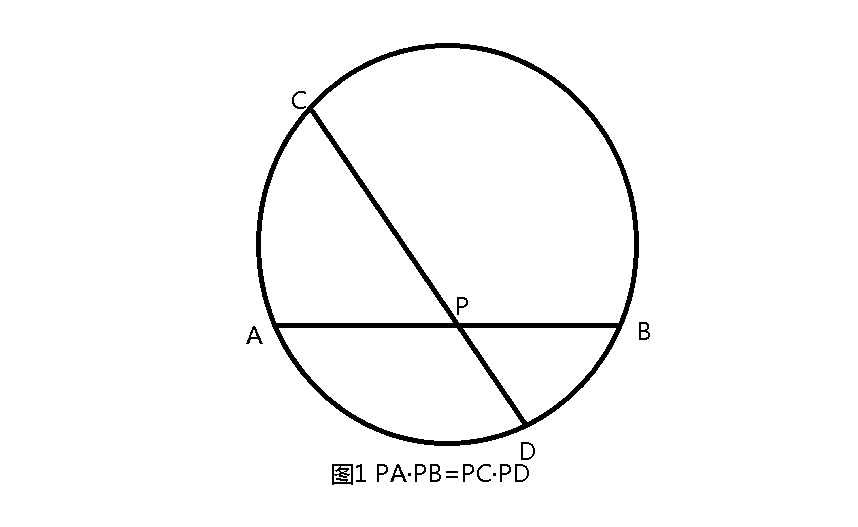
2.切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项。

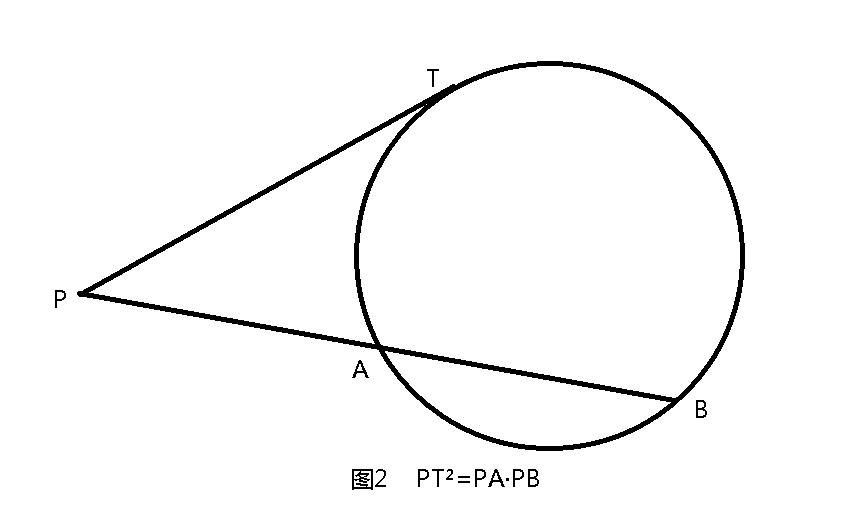
3.割线定理：从圆外一点引圆的两条割线，这一点到每条割线与圆交点的距离的积相等。

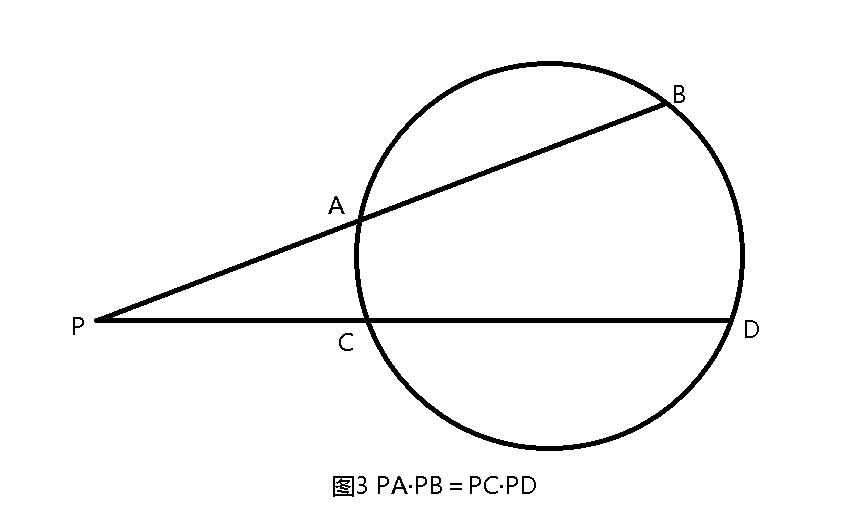
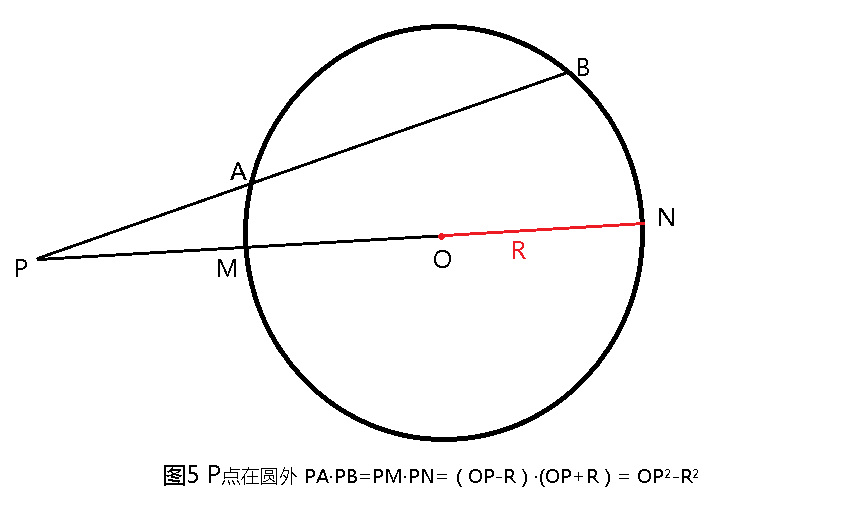
以上定理为什么称为圆幂定理呢？我们过平面上一个定点P，任作一直线与半径为R的定圆交于A、 B两点，则PA· PB为定值K，且等于∣OP²- R²∣，定值K称为点P对圆O的幂，简称"圆幂”（图4-5）。可以这样理解，圆幂是指平面上任意一点到圆心的距离与半径的平方差, 当点在圆外时,可以是切线的长度的平方,而切线的平方本身就是个“幂”,所以为了简化叙述,将与圆有关的切割线定理、割线定理、相交弦定理统称为“圆幂定理”。

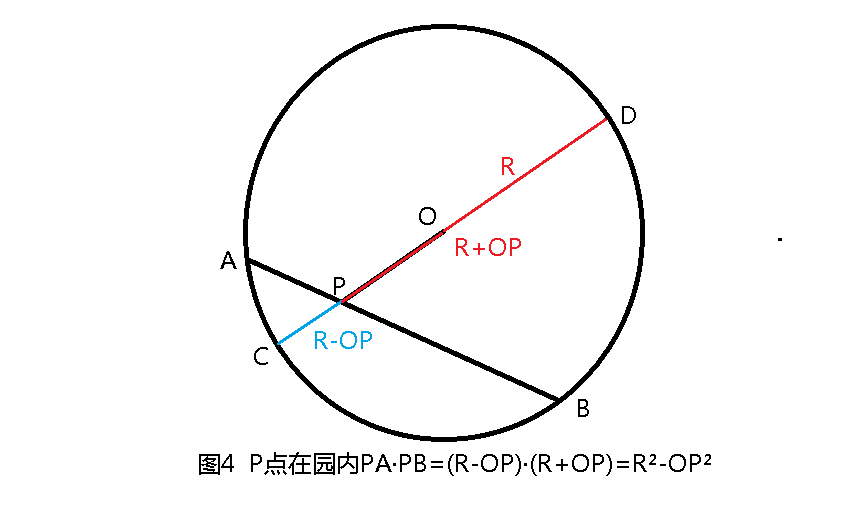
从汉字上理解，“幂”原指盖东西的布巾。数学中“幂”是乘方的结果，而乘方的表示是通过在一个数字上，加上标的形式来实现的，如3³、mⁿ，这就像在一个数上“盖上了一头巾”，所以叫做幂。

在我国，公元263年（南北朝时期）幂字第一次在数学文献上出现，数学家刘徽为 《九章算术》作注，在《方田》章求矩形面积法则下面写道：“此积谓田幂，凡广从相乘谓之幂”（长和宽相乘的积叫幂），也就是长方形的面积叫幂。到了公元656年，唐代数学家李淳风重注《九章算术》，在卷九《勾股》章中指出幂是边自乘，这时长方形变成了正方形，而作为面积的数学名词“幂”等于边长的自乘。公元1607年，明末的徐光启（1562一1633） 翻译欧几里得《几何原本》，徐光启使用“幂”，在书中给幂字下注解“自乘之数曰幂”。可见在数学上称幂在我国己是历史悠久，充分体现了古代中国人的聪明才智及丰富的想象力。